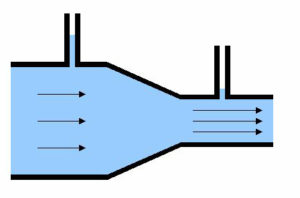
Představte si potrubí, ve kterém teče voda. Nás bude zajímat jeden jeho kousek, místo, kde se na širší trubku napojuje trubka užší. Voda proudí z širší do užší. Ve škole jsme se učili, že v tomto případě je v užší trubce nižší tlak, než v té širší. Ale proč? Logicky by se přece zdálo, že v té užší části bude přece voda víc natlakovaná, protože musí zvládnout protéct stejným jednotkovým objemem užší průměr. Jenže už tahle věta ukazuje, jak máme pojmy kolem tlaku, objemu a energie spletené v jeden téměř gordický uzel.
Podívejme se nejdřív na samotnou vodu v klidu.
Naše obvyklá představa nějakých malých kuliček, které jsou kousek od sebe a mohu se relativně volně pohybovat a klouzat po sobě není až tak špatná. Tady ale nesmíme zapomenout na jednu věc, že ty kuličky jsou od sebe daleko právě tak akorát – resp. nemohou být blíž. Pro naše vysvětlení si musíme připomenout jednu známou vlastnost: voda je (téměř) nestlačitelná (můžete ověřit i pokusem např. s injekční stříkačkou).
Teď se podívejme, co je to vlastně ten tlak.
(Nebudeme uvažovat hydrostatický tlak, tj. tlak vody v horních vrstvách na ty spodní, který způsobuje naše oblíbená gravitace). Pro názornost si představte nádobu plnou vody na horním konci uzavřenou pístem. Teď se vodu v nádobě pokusíme přece jen stlačit, třeba tak, že na píst položíme závaží. Voda se nestlačí (je přece nestlačitelná, že), ALE:
1) kdybychom nějakou trubkou propojili naši nádobu s turbínou hydroelektrárny, proudící voda by mohla turbínu roztočit,
2) kdyby závaží na víku bylo větší, voda by (do hydroelektrárny) proudila jaksi „prudčeji“ a třeba bychom mohli vyrobit více elektřiny,
3) kdyby záváží bylo extrémě těžké, nádoba by to nemusela vydržet a mohla by někde prasknout.
Náš pojem tlaku tedy vyjadřuje jakousi tendenci nebo ochotu vody v nádobě konat užitečnou práci – roztáčet turínu nebo trhat stěnu nádoby – v podstatě „být raději někde jinde, než se mačkat s ostatními (molekulami)“.
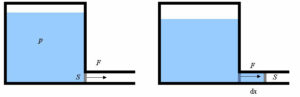
Pozn: Ve fyzice se tlak definuje jako síla působící v určitém místě na plochu ( p = F / S ). To je sice hezké, ale nic moc to neříká – jaká je tam tedy síla? Lépe je to vidět, když přibereme do hry ještě energii (tlakovou), což není nicjiného než možná práce, kterou může natlakovaná kapalina vykonat. Mějme nádobu s kapalinou pod tlakem p. U dna (opět zanedbejme hydrostatický tlak způsobený tíhou vody v gravitačním poli, nádoba je malá a kapalina pod větším tlakem než hydrostatickým) máme trubku s pístem.
Pokud píst odblokujeme, posune se díky síle F (ať už je jakákoli) o dx a kapalina pod tlakem tak vykoná práci
W = F . dx.
protože síla ale podle definice tlaku je
F = p . S,
je vykonaná práce (a tudíž tlaková energie, která se do ní převtělila) rovna
E = W = p . S . dx = p . (S . dx) = p . dV,
což je sympatické, ne?.
Samozřejmě, že věc je trochu složitější, dV musí být skutečně malé, protože když už kapalina nějakou práci uskuteční, klesne samozřejmě tlak, takže další posun se už děje s menší silou F, a tak dále. Nám bude ovšem stačit přímá úměrnost tlaku a potenciální tlakové energie.
Nyní pojďme k vodě, která proudí – čili do trubky.
Co se děje s její rychlostí při přechodu z širší trubky do užší? Protože nám ani na začátku ani na konci žádná voda nechybí (naše myšlenková experimentální aparatura je dokonale těsná, vodu nám nikdo nekrade ani není v užší trubce více nahuštěná), musí protéct za jednotkový čas stejné množství vody jak tou širší částí, tak tou užší. To je možné jedině tak, že voda v užší trubce proudí rychleji než v širší.
Tohle se ve fyzice odborně nazývá (S je průřez trubky a v rychlost)
rovnice kontinuity: S . v = konst,
ale v podstatě to není nic jiného než zákon zachování hmotnosti – asi…). Proudící voda má zcela určitě rychlost a tedy i kinetickou energii, rovnou
E = 0,5 . m . v2,
kterou by naše hydroelektrárna mohla jistě také využít (např. typický vodní mlýnek v proudu). Potenciální energie vody proudící v trubce je tedy složená z tlakové a kinetické složky. (Ta tlaková se rovnala podle našeho pokusu s pístem
E = p . V
Nyní na základě příslušného odstavce zákona zachování energie v platném znění: proudící kapalina pod tlakem má jakousi potenciální energii, která může být přeměna na užitečnou práci (stačí trubku jen vhodně napojit) – ta má svou kinetickou a tlakovou složku. Tato potenciální energie se nám nikde v trubce nemůže ztratit (může, vnitřním třením a zvýší se tím teplota vody, ale to zanedbejme, na věci by to nic nezměnilo).
Na jednotkový objem tak připadá (při daném tlaku a rychlosti proudění) stále stejná potenciální energie! Jestliže je ale v užší části větší rychlost, musí být i kinetická energie větší právě na úkor tlakové složky. A tlaková energie je přímo úměrná tlaku a objemu, objem je jednotkový a tudíž stejný, proto musí být menší tlak.
(Čímž jsme vynalezli světově známou
Bernoulliho rovnici: p . V + 0,5 . m . v2 = konst.,
a celá věc je tím vyřízena.
Další informace lze nalézt v příslušných kapitolách učebnice fyziky pro první ročník gymnázia.
Pozn. autora:
Pokud ještě nevěříte, zamyslete se nad následující otázkou: Co by se stalo, kdyby kinetická energie v užší trubce vzrůstala (roste přece rychlost při jednotkové hmotnosti) a zároveň tlaková energie zůstala stejná? Měli byste P——-m m—-e. Stačilo by trubku zužovat a zužovat, na konec postavit tu hydroelektrárnu, pomocí vyrobené elektřiny vodu v nejširší trubce vhodně natlakovat a pak už jen inkasovat faktury.